“学海拾珠”系列之五十五:因子动量与行业动量,孰因孰果?
由crisvalentine创建,最终由crisvalentine 被浏览 133 用户
报告摘要
主要观点
本篇是“学海拾珠”系列第五十五篇,本期推荐的海外文献研究了因子动量和行业动量之间的关系。研究发现因子动量与行业动量的表现形式相似,但因子动量强于行业动量,而且因子动量完全包含了行业动量。换句话说,因子动量是行业动量的原因,反之则不成立。即使同时控制个股动量、行业动量和Fama and French(2015)模型的五个因子,因子动量仍然强劲。
回到A股市场,虽然因子动量较难具有可投资性,但该文可以帮助我们更好地理解近年来A股市场的结构性行情,食品饮料、新能源等行业的强势表现是否可以归因于大盘成长等风格的因子动量值得深入研究,尝试通过跟踪特定因子动量的表现来预判热门行业的更迭。
- 因子动量是因子的一个共有属性,在经济和统计意义上均显著
几乎任何一组因子在经济上和统计上均表现出显著的因子动量。如果策略随机选择两个因子,做多上个月收益较高的因子、做空上个月收益更低的因子,其平均收益显著不为零。因此,因子动量是因子的一个共有属性。同时某些因子对因子动量策略盈利的贡献明显大于其他因子。其中,与财务困境、非流动性和波动性相关的因子最为重要,并且没有因子会显著降低因子动量策略的盈利能力。
- 因子动量不会推动个股收益产生短期反转或动量效应
因子动量不会推动个股收益产生短期反转或动量效应。实际上,当作者测量股票相对于其行业和因子暴露的回报时,与短期反转对应的t值从4.19增至14.39。当剔除短期反转和因子动量的影响后测量股票回报时,与短期反转对应的t值从4.31增至8.08。也就是说,除了行业和规模-B/M动量之外,因子动量并没有解决股票横截面收益中的其他难题。
风险提示
本文结论基于市场数据推测,不构成投资建议。市场风格大幅切换,可能导致基金经理持仓风格发生变化,本文结论仅供参考。
\
简介
行业表现出类似于股票横截面回报中的收益动量。Moskowitz and Grinblatt (1999)的研究表明,动量效应在一个月的时间范围内最强,但持续时间长达一年。作者使用文献中51个因子的数据作为股票收益的重要预测因子进行研究,结果显示因子动量的效应强于行业动量,因子动量完全包含行业动量,其传导机制是基于行业因子暴露的差异性。
首先,作者提出行业动量源于因子动量的假设,而检验这一假设的关键在于证明动量效应的传播方向。行业可以被表达为因子轮动,而因子也可以被表达为行业轮动。如果因子附带行业风险,那么行业冲击就会通过改变因子的行业暴露,进而影响因子收益(Asness, Frazzini, and Pedersen (2014))。这样看来,因子动量可能是源于行业动量的,而非作者假设的那样。为了论证假设是正确的,作者将因子行业中性化。即因子进行行业标准化,减去行业均值,再除以行业标准差,通过消除行业权重上的差异,消除由行业差异产生的偏配(Novy-Marx (2013))。此时因子与过往的行业收益无关,而未来因子收益与行业收益冲击仍旧正交。
因子动量包含行业动量,但行业动量不包含因子动量。在控制了个股动量和Fama-French五因子后,一个行业动量策略在一个月的构建与持有期下,获得了8.6%的年化回报率(t值=4.09)。然而,在控制因子动量的情况下,这一策略的alpha接近于零。这意味着,一旦控制了行业调整后的因子动量,未调整因子的历史回报将不再能预测未来的回报,行业中性化的因子动量包含了行业动量。相反,当作者控制了个股动量、行业动量以及Fama-French五因子时,所有构建与持有期在一个月到六个月内的因子动量策略都获得了正收益,其中表现最好的为一个月期限的策略。这个策略产生的alpha为每月32个基点,t值为3.85。因此,行业动量不包含因子动量。
因子动量还包含着在其他分散的投资组合收益中存在的动量。Lewellen(2002)发现,在25个按规模和账面市值比分类的投资组合中,存在着与行业动量相似的横截面动量,且规模和账面市值比上的动量与行业动量不同,两者互不包含。因子动量既包括行业动量,也包括规模和账面市值比因子的动量,且因子动量传输至二者的矢量相同。由于按规模和账面市值比分类的投资组合的因子暴露存在差异,因子动量传输到了投资组合的横截面收益中。
作者表明,之所以能用因子动量解释行业动量,并不是因为对因子的选择。因子动量不是由单一因子造成的,几乎存在于任何一组因子中。作者基于Fama-French五因子说明了这一结论。一个做多前一个月回报率最高的因子,做空回报率最低的因子的策略(横截面策略),获得了8.0%的年化平均回报,其t值为3.30。但策略的五因子alpha值更高,达到了每年10.7%的回报(t值=4.37)。而且该策略向获得高回报的因子轮换,将比横截面策略获得更高的回报。作者还构建了大小不一的随机因子集。使用一个随机的因子集(比如说10个因子)交易的策略,其盈利能力与包含全部因子的集合几乎相同。事实上,一个通过随机两个因子交替使用来捕捉因子收益动量的策略,通常结果也是显著的。即使因子只交易大市值股票,或者作者在构建期和持有期之间引入交易延迟机制,其效果仍然显著。
各个因子对因子动量收益的贡献不同。虽然交易全部51个因子的策略已经获得了较为显著的平均回报率(t=5.55),但其中一些因子组合产生的动量收益的t值甚至超过了8.0。作者通过测量各个因子从被交易的因子集合中移除时,收益受到多大的影响,来估计每个因子的“动量得分”。一个因子越重要,该策略的收益减少的幅度就越大。作者发现,虽然没有因子明显降低了收益,但一些因子对因子动量收益的贡献要明显大于其他因子。比如,与困境、非流动性和异质性风险有关的因子就是对因子动量收益贡献最大的因子之一。对收益有着最大的贡献的因子不一定具有最强烈的动量效应。例如,动量得分较高的公司年龄(Barry and Brown (1984))因子和名义股价(Blume and Husic (1973))因子,在1963-2016年的样本期上的动量效应表现很弱。
行业动量和因子动量都与短期反转(Jegadeesh(1990))密切相关。在一个月的时间窗口上,反转因子对股票收益的预测是负向的,而行业和因子动量对收益的预测为正向的。因此,短期反转是一种与行业相关的效应,基于与行业平均水平相关的股票收益率会使预测因子更为强大(Da, Liu, and Schaumburg 2013;Novy-Marx and Velikov 2016)。事实上,虽然短期反转因子的五因子alpha为每年6.1%(t值=3.61),但当作者控制行业动量时,这一alpha增加到10.2%(t值=8.44)。如果作者还控制因子动量,短期反转的alpha为12.6%(t值=12.85)。UMD的五因子alpha值为每月72个基点(t值=4.31),而当该策略不存在短期反转或因子动量上的风险暴露时,其alpha值增加到了136个基点(t值=8.08)。因此,因子动量不是股票动量产生的缘由,当作者控制因子动量时,股票动量增长得更快。
作者的结论可以对分散化投资组合中动量收益的来源产生新的见解。例如,行业动量源于因子动量的发现排除了一些先前对行业动量的解释。行业动量不是由于对特定行业新闻的反应不足,因为行业调整后的因子不会产生特定的行业暴露。如果因子动量是由于对信息的反应不足,则该信息必须位于因子层面。如果因子与宏观经济风险有关,那么市场肯定对宏观经济信息反应不足。另一方面,Stambaugh and Yuan(2016)认为许多因子可能与错误定价有关。
数据
CRSP和Compustat
作者使用证券价格研究中心(CRSP)提供的在纽约证券交易所、美国证券交易所和纳斯达克上市的普通股票和退市股票的月度和日度回报数据。如果一只股票的退市回报缺失并且退市与业绩相关,作者将纽约证券交易所和美国证券交易所股票的回报推算为-30%(Shumway1997),纳斯达克股票的回报推算为-55%(Shumway and Warther1999)。
作者从年度Compustat文件中获取会计数据,并遵循标准惯例将会计信息滞后六个月(Fama and French1993)。例如,如果一家公司的财政年度在t年的12月结束,作者假设投资者可以在t+1年的6月底获得此信息。
作者计算了1963年7月至2016年12月的因子回报,但一些诸如异质波动率和市场beta的预测因子的计算,使用了一些1963年以前的回报数据。
因子的构建
表1展示了作者在研究中检验的51个因子的平均回报以及三因子和五因子模型调整后的alpha。在表1中,作者将因子分为两组。基于会计的预测因子使用利润表或资产负债表信息;基于股票回报的预测因子使用回报、价格或交易量数据。
作者通过按市值和收益将股票分为六个投资组合来构建每个类似HML的因子。作者使用NYSE上市股票的市值中位数以及预测因子的30分位数和70分位数在两个维度中独立排序。作者计算了六个投资组合的市值加权回报。一个因子的回报是两个市值分位组中因子多头投资组合的平均回报减去两个因子空头投资组合的平均回报。在分配股票给高和低的投资组合时,作者标记回报预测因子,以使高投资组合包含原始研究中确定为获得较高平均回报的那些股票。作者在每年6月底重新平衡基于会计数据的因子,并每月重新平衡基于回报数据的因子。
表1的左侧展示了标准因子的平均回报、alpha值和t值;右侧报告了行业调整因子。标准因子按未调整的回报预测因子对股票进行排序。在构建行业调整因子时,作者首先调低49个Fama-French行业的预测因子。每个因子的多头和空头在各个行业中大致均匀分布。然后作者通过在每只股票的市值加权行业中建立抵消头寸来对冲任何剩余的行业风险;也就是说,如果一个因子在股票i中持有多头头寸,它也会在股票i的行业中持有相同数量的空头头寸。经过调整,这些行业调整因子的过去回报与行业回报无关;因为回报是行业中性的,未来的行业回报也不会影响因子回报。这种行业调整因子的定义与Novy-Marx(2013)使用的相同。
表1中平均回报与三因子模型alpha之间的比较表明,在控制市值和账面市值比时,某些因子的表现明显更好。例如,Novy-Marx(2013)的总盈利能力在控制账面市值比不变时是一个特别强大的回报预测指标。它的月度平均回报仅为21个基点(t值=2.35),但三因子模型alpha值为38个基点(t值=5.36)。
标准因子和行业调整因子的比较表明,行业调整通常会提高因子表现(Cohen and Polk1996;Asness、Porter and Stevens2000;Novy-Marx2013),有时甚至会显著提高。例如,与短期反转相关的五因子模型alpha为37个基点(t值=3.02)。相比之下,行业调整因子的alpha为每月74个基点(t值=9.24)。在不属于五因子模型的47个因子中,与行业调整因子相关的t值高38倍。
因子动量与行业动量
因子动量
横截面动量策略根据资产或资产组合在某个构建时期的相对回报来选择资产或资产组合。例如,在个股的横截面中,典型的策略衡量过去一年的回报(跳过过去一个月),并每月将股票分配到投资组合中(Novy-Marx2012)。这些策略跳过一个月是因为个股回报往往会在一个月的范围内具有反转效应。
作者遵循Jegadeesh and Titman(1993)以及Moskowitz and Grinblatt(1999)定义的因子动量策略。每个月作者都会根据前L个月期间的平均回报对因子进行排名,然后在表现最好和最差的因子上建立多头和空头头寸。该策略在每个多头和空头的因子上投资等量。然后作者在接下来的H个月内持有这种策略。因此,每个策略都由L/H对描述。作者还需要指定策略持仓的因子数量。Moskowitz and Grinblatt(1999)使用20个行业组合,并在前三名和后三名行业中持有多头和空头头寸。作者遵循了这个规则,让因子动量策略在建立多头和空头头寸在
个因子中,其中N是因子的个数。作者的完整集合有51个因子,但接下来会考虑N从2到50范围的子集。
当持有期超过一个月时,即H>1,持有期收益重叠。作者使用Jegadeesh and Titman(1993)方法来重组数据以解决这种重叠问题。例如,当持有期为H=3个月时,作者在每个t月形成因子动量策略,并计算该策略在t+1、t+2和t+3个月的收益。例如1999年1月,作者得到了在三个不同时间形成的三种策略的回报:一种是在1998年12月末形成的,一种是在1998年11月末形成的,最后一种是在1998年10月末形成的。三个月持有期策略是这三种策略的平均回报。对此策略的一种解释是每月重新平衡三分之一的投资组合(Jegadeesh and Titman1993);另一种解释是,这个过程只是重塑数据以避免使用重叠的观察结果。
表2检验了四种因子动量策略,前两个基于标准因子,后两个使用行业调整因子。作者使用一个月的构建和持有期(L=1,H=1)以及六个月的构建和持有期(L=6,H=6)。这些策略基于所有的51个因子,因此每个策略根据等式(1)中的规则在最高和最低的8个因子中持有多头和空头头寸。
A部分显示了四种因子动量策略在1963年至2016年样本期间均获得了统计上显著的平均回报。当构建期和持有期均为1个月时,标准因子策略每年平均收益率为10.5%,标准差为15.3%;基于行业调整因子的平均回报率为6.4%,标准差为8.4%。由于标准差的差异,与行业调整策略相关的t值5.55超过了与使用标准因子的策略相关的t值5.01。同样,在六个月的构建和持有期中,行业调整策略优于未调整策略;t值分别为4.05(行业调整因子)和2.05(标准因子)。
表2中B部分展示了来自生成测试的估计,这些测试检查了行业调整和标准因子动量策略的增量信息内容。在这些回归中,作者控制了Carhart(1997)Fama and French(2015)五因子模型的市场、市值、价值、盈利能力和投资因子和其他因子动量策略。例如,第一个回归使用一个月的构建和持有期,并解释了标准因子动量策略中的时间序列变化,其中五因子模型增加了个股动量因子。统计上显著的截距表明左侧因子包含右侧因子未涵盖的信息(Huberman and K and el1987;Barillas and Shanken2016)。也就是说,如果截距在统计上显著不等于零,则已经交易右侧因子的投资者可以通过将其向左侧因子倾斜来提高其投资组合的夏普比率。
B部分中的估计量表明,行业调整的因子动量策略包含未调整的因子动量策略,但反之则不然。例如,尽管具有1个月构建和持有期的未调整策略的六因子模型alpha值为每月85个基点(t值=3.84),但当作者控制行业调整因子动量时,其alpha值降至-3个基点。该截距在统计上不显著,t值=-0.28。对于六个月的构建和持有期,估计的年化截距为-20个基点,t值=-3.07。A和B部分中的估计量表明动量存在于标准和行业调整因子中,但行业调整因子动量包含未调整因子中的动量。作者在之后涉及的的每个因子动量策略都以行业调整因子为准。
图3展示了不同因子动量策略的平均回报以及五因子和六因子模型alpha相关的t值。作者按构建和持有期从1个月到6个月不等,构建了36种策略。五因子模型包括Fama and French(2015)的市场、市值、价值、盈利能力和投资因子,六因子模型增加了Carhart(1997)的个股动量策略。
A和B部分显示,当以平均回报和五因子模型alpha值衡量时,所有因子动量策略都会产生统计上显著的收益,而且两者之间的差异通常很小。例如,L=1,H=1策略的年化平均回报率为6.4%(t值=5.55)。该策略的年化五因子模型alpha为6.6%,t值=5.62。面板A和面板B之间的相似性表明,类似于股票动量(Fama and French2016),因子动量在很大程度上与市场、市值、价值、盈利能力和投资因子无关。
图3中的C部分显示股票动量与因子动量显著相关。尽管在添加股票动量因子的六因子模型中,与L=1、H=1策略相关的年化alpha值为6.6%(t值=5.53),但其他alpha值均大幅下降。一个月构建和持有期的策略不受影响,因为与因子动量不同,股票动量的计算跳过过去一个月的收益。在控制股票动量后,6个月构建期和持有期的策略的alpha在统计上不显著;每年仅0.7%,t值=1.09。此外,即使持有期超过1个月,alpha仍然显著,因为这些持有期也包含t+1月份。例如,L=1,H=3策略总是在具有一个月构建和持有期的策略中投资1/3。在讨论了行业动量之后,作者将分析缩小到具有一个月构建和持有期的因子动量策略。
行业动量
表4中的A部分展示了使用1个月或6个月构建和持有期的行业动量策略的年化平均回报和标准差。作者使用20个Moskowitz and Grinblatt(1999)的行业,每个策略在最高和最低三个行业中持有多头和空头头寸。一个行业的回报,如Moskowitz and Grinblatt(1999)所述,是其股票的市值加权回报。行业动量策略买卖这些行业的等权重投资组合。表4中的策略与Moskowitz and Grinblatt(1999)研究的策略相同,只是作者的样本周期更长。图5与图3类似,报告了与36种行业动量策略相关的t值,这些策略是按构建和持有期从1个月到6个月不等构建的。
所有版本的行业动量都会产生正的平均回报和五因子模型alpha值。与因子动量类似,基于一个月构建和持有期的策略脱颖而出。其年化五因子模型alpha值为10.2%(t值=4.85)。该策略也是唯一一种在六因子模型中保持其alpha统计显著的策略。控制股票动量,其他35种策略中的最高t值为1.84。
在图5中,作者将负t值展示为零。在某些情况下,这些负alpha具有统计显著性。例如,L=5,H=5策略的六因子模型alpha为-3.3%(t值=-2.44)。这些负的估计量表明,结合股票动量来交易对冲某些形式的行业动量将是有益的。因此,该结果与表1中标准动量因子和行业调整动量因子之间的差异一致。标准动量因子的五因子模型alpha的t值为4.31;行业调整版为5.70。Asness、Porter and Stevens (2000)还指出,当按行业相对回报排序时,股票动量会变得更强。
因子动量包含行业动量。表4展示了回归的估计量,其解释了五因子模型、股票价格动量和因子动量的行业动量的时间序列变化。与1个月和6个月行业动量策略相关的每月alpha值为0.17%(t值=1.15)和-0.20%(t值=-1.77)。它们对因子动量策略的载荷为0.99和0.38。在图6的A部分中,作者展示了与各种行业动量策略七因子模型的alpha相关的t值。该图表明,除了构建和持有期为一个月的策略外,其他35个行业动量策略在控制股价和因子动量时均不具有统计上显著的正alpha。
行业动量并不包括因子动量。图6的B部分数据显示,在一个月构建期和持有下,因子动量策略比行业动量策略获取了更多的回报信息,其年化alpha为3.9%(t值=3.85)。而且在控制了股票动量之后,行业动量并没有改变因子动量策略的盈利能力。如果有的话,包含Fama-French五因子、股价动量和行业动量的七因子模型t值会高于除不控制行业动量之外相同模型的t值(图5的C部分)。
表4还检验了按市值和账面市值比排序的25个Fama and French(1993)投资组合轮动的动量策略的表现。A部分显示,与Lewellen(2002)的发现一致,这种动量策略收益也是较高的。一个月构建和持有期的策略平均年化回报率为9.1%(t值=4.75),接近于行业动量策略所获得的回报。B部分显示,与行业动量类似,该策略也包含因子动量。一个月构建期和持有期的与市值和B/M动量策略相关的七因子模型alpha值为每月6个基点(t值=0.49)。而且,与行业动量类似,规模和B/M动量不包含因子动量。控制规模和B/M动量下,B部分中因子动量策略的alpha为每月28个基点(t值=3.74)。
不同时间的因子动量、行业动量和股票动量
图7分别呈现了1963年到2016年期间,因子、行业和股票动量策略的累积对数回报。作者将这些策略与五因子模型进行正交,收益是投资者仅持有单个形式的动量所产生的。为使每个因子的波动率与行业动量策略的波动率相同,作者对每个因子进行杠杆化或去杠杆化处理。比如,表2和表4显示,使用一个月构建期和持有期的策略的年化标准差为9.3%(因子动量)和14.8%(行业动量),因子动量策略的波动性大大低于行业动量策略,所以需要杠杆化。图7还呈现了市场因子的累积回报,同样,为了与行业动量策略的波动性相匹配,它的波动性也需要被杠杆化。
在1963年至2016年期间,三个动量策略都获得了明显高于市场的回报(扣除五因子模型的影响)。但它们的表现在2000年左右就出现了很大的差异。主要由于金融危机期间的动量崩溃,从2000年开始直到样本期结束,行业动量和股票动量的累积回报率约等于零。Barroso and Santa-Clara(2015),Daniel and Moskowitz (2016),以及Moreira和Muir(2017)表明,投资者可以通过观察策略的波动性增加来预测这次崩溃;在2000年后的样本中,波动性管理的股票动量策略的α值明显为正。
因子动量与股票和行业动量不同,特别是在样本期的末尾。在个股动量出现失效的时候,因子动量的收益经历了一次上跳。即使没有这次上跳,因子动量在2000年前后的回报相当。尽管其有时表现不佳——例如,它在1965年和1990年前后的回报都是平的或负的——但它的正异常回报长期来看仍显著。
\
敏感度分析
备选因子集
到目前为止,作者已经使用了表1中列出的所有51个因子来形成因子动量策略。因子对因子动量的贡献可能不同。例如在个股回报方面,Avramov、Chordia、Jostova and Philipov(2007)表明,信用评级较低的股票的动量更强。
表8显示,作者关于因子动量的结果对因子集的选择不是很敏感。在表中,作者从四组因子中构建了具有一个月构建和持有期的策略。第一组包括所有因子;第二组包括38个财务因子;第三组包括13个盈利因子;第四个包括Fama and French(2015)模型的五因子。使用Fama-French五因子的策略包含了其他几组中都不包括的市场因子。
表8中的每个因子动量策略都获得了统计上显著的正回报。例如,使用Fama and French(2015)模型五因子轮动的1个月期限策略,在t值为3.30的情况下获得月平均67个基点的回报。该策略衡量市场、市值、价值、盈利能力和投资策略相对上一个月的表现,并在表现最佳和最差的因子中建立多头和空头头寸。财务因子轮动策略相比盈利因子表现得更好。尽管后者的平均回报(69个基点)超过了前者(38个基点),但交易财务因子的策略的波动性较小;两种策略的t值分别为5.71(基于财务因子)和4.38(基于收益因子)。交替使用全部51个因子的策略的表现与基于财务因子的策略相当。
因子动量策略可以通过Conra and Kaul(1998)提出的平均回报机制获得正回报。Conrad and Kaul(1998)指出,如果平均收益存在差异,通过出售低收益资产来购买高收益资产的策略自然会倾向于高平均收益的资产。为了证明这个结论,假设作者构建了一个只在两个因子中建仓的策略。如果第一个因子的平均回报率远远超过第二个因子,那么动量策略通常会做多第一个因子,做空第二个因子。但是由此产生的正平均收益,只是由于该策略对高平均收益因子的静态倾斜。如果已实现的1个月或6个月回报足以提供关于平均回报差异的信息,那么该机制可以解释因子动量策略的收益来源。
Fama-French五因子的详述表明,该策略的任何回报都不是来自于静态因子的暴露。表8展示了与该策略相关的五因子模型的alpha。这个模型从结构上完美消除了所有针对正在交易的五个因子的静态因子暴露。因子载荷表明该动量策略对市场和盈利能力因子的暴露度为负,且没有因子的暴露度在统计上显著为正。该策略的月度五因子模型的alpha为89个基点(t值=4.37),超过了其67个基点的平均回报(t值=3.30)
在图9中,作者分析了策略结果对因子集合选择的敏感度。作者基于随机的因子集合,构建形成和持有期为一个月的因子动量策略,并记录所产生的t值。作者考虑了从51个因子的完整集合到只有两个因子的集合范围。当策略使用两个因子时,其基于两个因子在前一个月的表现,在回报率较高的因子中做多,在另一个因子中做空。对于每个集合大小,作者随机抽取了10000组因子。图9中的实线是这些模拟的平均t值;虚线表示95%的置信区间。这些线中的“结点”代表着由策略做多和做空的因子数量变化。作者让因子的数量根据公式(1)随着因子集合大小的变化而变化。
图9显示,即使因子数量从51个下降到25个,策略中与平均夏普比率成正比的平均t值也几乎不变。此外,即使只有几个因子,因子动量策略通常也是盈利的。因此,表8中基于Fama-French模型的策略结果并不是偏差;使用一组随机的五个因子,图9中的平均t值为3.92,自举95%置信区间从2.13到5.87。因此,因子动量是大多数因子的共有属性,即几乎任何随机因子集合都表现出动量。
哪些因子对因子动量有贡献?
图9表明,因子对因子动量策略利润的贡献可能不同。95%置信区间表明,一些随机因子组合产生的收益高于全部因子集合。事实上,表8显示,与使用全部51个因子相比,38个财务因子的轮动策略相对所有51个因子具有更高的t值。
在图9中随机抽取的一组因子中,最佳因子动量策略仅在六个因子之间轮动:公司年龄、短期反转、资产回报率、Altman的Z值、销售比价格和资产增长率。平均回报下,策略交易所有51个因子的t值为5.55(见表8),而交易这六个因子的的t值为8.47。寻找产生最高样本内t值的2到51个因子的组合是很诱人的;这个问题是一个非线性背包问题。然而,这样做会产生与使用大量资产构建事后均值方差有效投资组合时相同的问题。只要新资产的样本内回报没有被现有资产完美覆盖,该投资组合的夏普比率就会随着每项新资产的增加而增加。因此,作者在本节中衡量和测试每个因子对因子动量策略的利润贡献多少,然后研究由这些分数形成的各种因子动量策略的样本外表现。
表10呈现了各因子对因子动量策略收益贡献程度的得分。作者遵循三个步骤去计算各个因子的动量得分。
- 在一个月构建期和持有期上,作者构建基于随机十个因子的因子动量策略,并计算出策略的平均收益。
- 作者每次随机删掉十个因子中的一个,并基于其余九个因子构建一个策略,并计算相对于步骤(1)中初始十因子策略平均回报的减少值。
- 作者重复计算了25000个随机十因子集合。一个因子的动量得分为与平均回报平均减少相关的t值。作者将这些t值乘以-1,因此此数值越高的因子对因子动量策略收益的贡献越大。
动量分数衡量了每个因子对因子动量策略收益的增加程度。经济学的直觉是,如果作者去除其中一个因子时,因子动量策略的平均回报大幅下降,那么该因子是该策略利润的重要贡献者。
作者随机抽取10个因子,以确保结果对因子之间的冗余不敏感。否则为了说明可能出现的问题,需要考虑盈利能力因子占因子动量利润的很大贡献比例的可能性。然而,由于最初列出的51个因子包括股本回报率、营业利润率、毛利润率等多种盈利能力指标,如果作者从完整的数据集开始测试,很难观察到盈利能力在数据中的重要性。如果作者删掉一个盈利因子,其他盈利因子可能会填补被删掉的因子的空缺。所以,最初的因子集越小,就越难出现因子冗余。
表10中A部分按动量分数列出了51个因子。这些分数的分布是不对称的。虽然9个因子的分数在10%水平上具有统计显著性,但没有一个因子在该水平上具有统计显著性的负分数。也就是说,某些因子比其他因子对动量利润的贡献更大,但没有任何因素会损害因子动量策略的表现。
对动量利润贡献最大的因子并不是平均回报最高的因子。例如,得分最高的因子是Barry and Brown(1984)的公司年龄(t值=4.57)。根据表1,该因子的五因子模型alpha为每月2个基点(t值=0.58)。相比之下,得分最低的因子(t值=-1.57)是Gervais、Kaniel and Milgelgrin(2001年)的高交易量回报溢价因子,其具有五因子模型alpha(t值=7.26)。
列表顶部因子的经济性与列表底部的因子不同。与财务困境相关的三个因子——Campbell、Hilscher and Szilagyi(2008)的困境风险、Ohlson(1980)的O-score和Altman(1968)的Z-score——都出现在上半部分列表;得分为2.27的杠杆也可能与财务困境有关。对因子动量利润的贡献得分较高的几个因子与非流动性和波动性有关;短期反转、异质波动率、市场beta、最大回报和Amihud的流动性不足等因素出现在列表的上半部分。
表10的B部分将表1中列出的51个因子分为五组,并展示了由此产生的因子动量策略的月平均回报和五因子模型加上UMDalpha。第一组包括根据A部分的分数对因子动量利润贡献最小的10个因子;第五组使用得分最高的10个因子。平均回报和t值的差异很大。在底部五分位数中,因子动量策略的平均回报为9个基点(t值=2.24);在前五分位数中,它是87个基点(t值=6.76)。因此,使用得分最高的10个因子的因子动量策略的表现超过了表8中考虑的任何子集。顶部和底部五分之一之间的平均回报和alpha差异在统计上是显著的,t值分别为6.92和6.38。
头部五分之一的因子动量完全涵盖了其他五分位数的因子动量。作者估计回归
对于五分位数q=1、2、3和4,衡量这些五分位数中因子动量策略对未来收益的增量信息;这里,FMOMqt是交易属于五分位数q的因子的动量策略的第t个月回报。与alpha相关的t值范围为从-1.52到0.17。也就是说,从1963年到2016年,所有因子动量策略的收益都可以通过在表10中A部分顶部列出的十个因子之间轮动获得。
样本外测试
表10表明,因子对因子动量收益的贡献不同,这些差异在经济和统计上都是显著的。这种分析的局限性在于它是在样本内完成的。作者使用1963年到2016年的时间段对因子进行评分,然后使用相同的样本衡量各种因子动量策略的表现。由于分数基于各个因子对因子动量策略的贡献,因此测试偏向于寻找表现间的差异性。也就是说,即使某些因子对因子动量收益的贡献大于其他因子只是偶然,表10也会收集此类偶然事件的影响。
作者本着Fama and French(2016a)以及Jegadeesh (2017)的思想,使用样本外数据来验证其结果不是偶然发生的。作者首先将样本分为奇数(t=1,3,...)和偶数(t=2,4,...)月,然后使用与上述相同的步骤,使用奇数月回报计算所有因子的动量分数。接着再次根据这些分数将因子分配到五分位数,并在偶数月内衡量这些策略的表现。即用于衡量绩效的回报与用于对因子评分的回报不重叠。最后,作者切换奇数月和偶数月来衡量因子动量策略的样本外奇数月表现,并将两个样本外回报序列结合起来,以获得涵盖整个样本期的样本外回报。
表10中B部分的样本外列显示,具有最高动量分数在样本外产生更高的因子动量收益。使用最低五分之一因子的策略可获得22个基点的平均月回报;顶部五分位策略的平均月回报为66个基点,顶部和底部五分位之间的差异显著,t值为3.44(平均回报)或3.14(五因子模型加UMD alpha)。
实施交易延迟和大小市值股票对比
因子动量,类似于行业和规模-B/M动量,在构建和持有期均为1个月时最为强劲。该策略是通过在t月最后一个交易日结束时将因子分类到投资组合中,并持有该投资组合至t+1月末最后一个交易日。在表11中,作者衡量了结果对投资者必须以收盘价交易的假设的敏感程度。
第一列是基准策略,其在t月最后一个交易日收盘时持有标的股票头寸,并持有这些头寸直到t+1月底。在表8的第二列中,作者跳过了一个交易日构建期和持有期。因此,这里的收益是从t+1月的第一个交易日结束到月底计算的。在接下来的两列中,作者在开始计算持有期回报之前跳过形成期后的两到三个交易日。
平均回报和alpha值随着作者扩大构建和持有之间的楔形下降。例如,当作者在延迟三个交易日后开始测量回报时,动量策略的平均回报是37个基点(t值=4.16)而不是53个基点(t值=5.53)。然而,这种收益下降在经济意义上是很小的,这是因为随着作者跳过几天,持有期的长度会减少。而第一列平均持有期的长度为21个交易日——一个月内平均交易天数的次数——跳过三天的持有期为18个交易日。因此,即使因子动量策略的收益在每个交易日相同,作者预计该策略的平均月回报率将从53个基点降至45个基点。表11中的估计量表明,因子动量策略的盈利能力并不主要取决于投资者以t月末的收盘价进行交易导致的。
表11中最右边的两列衡量了从小市值和大市值股票分别构建因子动量策略的盈利能力。例如,Fama and French(1993)的标准HML因子是这样构建的:首先根据纽约证券交易所的中位数将股票分为小市值和大市值股票,然后根据30和70纽约证券交易所的账面市值比分界点将股票独立地分为三个区间——价值、中性和成长。然后将HML因子的Month-t回报定义为
表11显示因子动量在小市值股票中更强,但并非特定于小市值股票。小市值因子动量策略的平均回报为63个基点(t值=5.39);在大市值因子动量策略上是33个基点(t值=4.08)。平均回报的差异超过t值的差异,因为小市值因子动量策略比大市值因子动量策略更不稳定。
短期反转与个股动量、行业动量和因子动量
行业动量和因子动量都与短期反转有关。Jegadeesh(1990))表明,在一个月的范围内,股票收益会对的股票横截面收益进行负向的预测,而行业和因子会对其进行正向的预测。这是因为,短期反转与动量的作用方向相反。此外,它们还会增强对方的效应。作为行业动量的结果,短期反转是一种与行业组合相关的效应。与行业组合相关的股票回报率,其预测作用明显比原始回报率更强(Da、Liu and Schaumburg(2013)以及Novy-Marx and Velikov(2016))。图3的结果也明显符合这一结论。初始短期反转因子的五因子模型alpha为每月37个基点(t值=3.02),而经过行业调整后,alpha上升至每月74个基点(t值=9.24)。
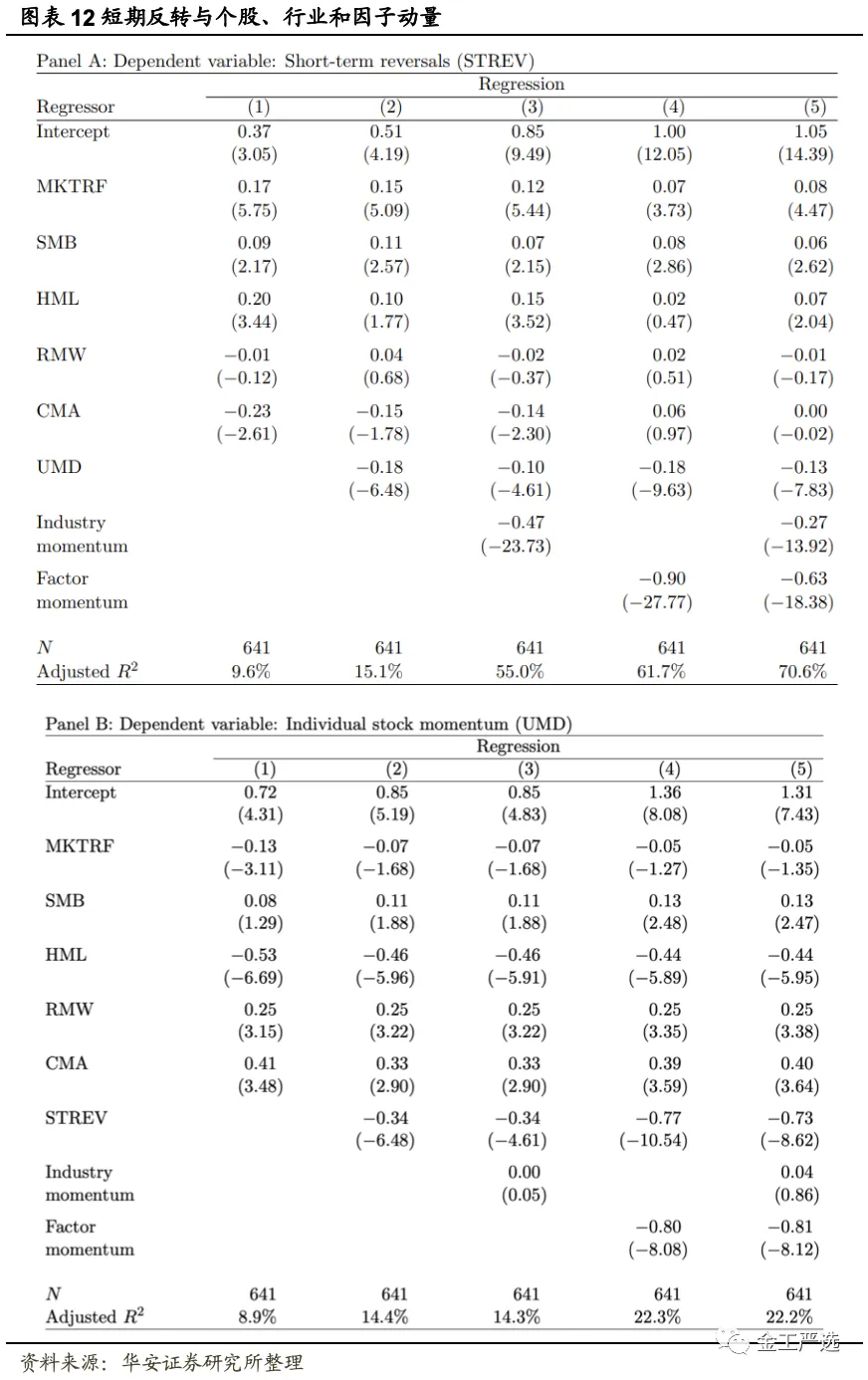
在表12的A部分,作者研究了短期反转、行业和因子动量的关系。作者估计跨度回归,其中因变量为短期反转因子的月度回报,自变量为Fama-French模型的五因子、Carhart(1997)的股票动量因子、行业动量与因子动量策略的月度回报。左侧变量是标准的,即未经调整的短期反转因子。行业和因子动量策略是表2和表4中报告的具有1个月构建和持有期的策略。
表12中的跨度回归测量了当短期反转因子相对于行业和因子动量正交为中性时,月度股票收益的信息内容变化的程度。例如,五因子模型alpha代表了做多短期反转因子,但同时在市场上持有回报、规模、价值、盈利能力和投资因子以使针对这些因子的净暴露为零。在同样控制股票动量(UMD)和行业动量的第三个回归中,投资者也交易这些因素以将其净暴露设置为零。此回归中的alpha为每月85个基点,t值为9.49。
最右边的两个回归表明,当这种效应对因子动量的净暴露设置为零时,短期反转在经济和统计意义上都显著增强。在仅具有因子动量的回归中,截距为每月1%,t值为12.05;在同时控制行业和因子动量的回归中,截距为每月1.05%,t值为14.39。
表12的B部分显示因子动量也与个股动量有关,但方向相反。UMD的五因子模型alpha为每月72个基点,t值为4.31,当我们将短期反转和因子动量添加到五因子模型时,该alpha几乎翻倍至136个基点(t值=8.08)。相比之下,这与个股动量无关。在表12的回归中,它的斜率小于零。
这些影响的经济规模很大。例如,考虑股票动量(UMD)因素。该因子的五因子模型alpha为每月72个基点,五因子模型残差的月度标准差为4%。因此,UMD的五因子模型的年化信息比率为0.62。相比之下在表12A部分的最后一列中,短期反转的信息比率为2.13。也就是说,当策略对行业动量与因子动量持中性,且短期反转因子的标准偏差为10%时,该策略将带来21.3%的交易成本前回报。同样,当策略对短期反转和因子动量持中性时,与股票动量相关的信息比率从0.62增加到1.27。
表12中A部分中的估计表明,因子动量显著增强了短期反转的经济意义。预测回报的不仅是股票相对于其行业的回报,而且是消除了因子暴露之后的。相似的,推动个股回报动量的机制也必定不同于产生因子动量的机制。如果这两种效应来自同一个源头,当作者控制因子动量时,个股的回报动量应该会减弱。相比之下,表12中B部分显示动量效应变得更强。
 结论
结论
Jegadeesh and Titman(1993)的研究表明,过去一年的股票收益可以用于预测当期股票的横截面收益。之后的研究还表明,其他资产类别同样存在动量效应,并且能够长期持续(Asness, Moskowitz and Pedersen(2013))。Moskowitz and Grinblatt (1999)研究发现:与股票的动量效应不同,充分分散的行业组合中存在动量效应,并且基于过去一个月时间窗口的短期动量效应非常明显。
本文研究表明因子动量方式与行业组合动量表现方式相似,但因子动量强于行业动量,且因子动量完全包含了行业动量。通过行业调整后的因子,作者发现因子动量是行业动量的原因,而并非行业动量是因子动量的原因。即使同时控制股价动量、行业动量和Fama and French(2015)模型的五个因子,因子动量仍然强劲。因子动量还包括按规模和账面市值比排序的投资组合动量(Lewellen2002),反之则不成立。
几乎任何一组因子在经济上和统计上均显示出显著的因子动量。例如,仅根据过去一个月收益构建的Fama and French(2015)模型的五因子轮动策略,其年化alpha为10.7%(t值=4.37)。实际上,如果随机选择两个因子,做多上个月收益更高的因子、做空上个月收益更低的因子这一策略的平均收益显著不为零。因此,因子动量是因子的一个共有属性,同时某些因子对因子动量策略盈利的贡献大于其他因子。与财务困境、非流动性和波动性相关的因子最为重要,并且没有因子会显著降低因子动量策略的盈利能力。
因子动量不会推动个股收益产生短期反转或动量效应,仅是显著增强了这两种效应。实际上当作者测量股票相对于其行业和因子暴露的回报时,与短期反转相关的t值从4.19增加到14.39。当剔除短期反转和因子动量后测量股票回报时,与个股动量相关的t值从4.31增至8.08。即除了行业和规模-B/M动量之外,因子动量并没有解决股票收益横截面中的其他难题。
作者的结论可以对分散化投资组合中动量收益的来源产生新的见解。例如,行业动量源于因子动量的发现排除了一些对行业动量的解释。行业动量不是由于对特定行业新闻的反应不足,因为作者的行业调整因子不会持有特定行业暴露。如果因子动量是由于对信息反应不足,则该信息必须是因子层面的。如果因子与宏观经济风险有关,那么市场肯定对宏观经济信息反应不足。另一方面,Stambaugh and Yuan(2016)认为许多因子可能与错误定价有关。
文献来源:
核心内容摘选自Rob Arnott、Mark Clements等人在National Bureau of Economic Research上的论文Factor Momentum。
\
风险提示
作者结论基于历史数据与海外文献进行总结;不构成任何投资建议。